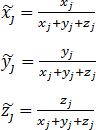
The method is used to calculate the VaR model.
Select distribution type for each financial instrument used in calculations:
Normal (Gauss) Distribution.
Student's Distribution.
Chi-Square Distribution.
Bilateral Exponential Distribution.
Weibull Distribution.
Gamma Distribution.
Uniform Distribution.
Financial instruments may have various distributions.
Depending on the distribution, correlate random values are generated for each financial instrument. Matrix of generated random values:
R = ǁRk,jǁ
Where:
k. The number of trials.
j = 1, 2, … M. The number of financial instruments included into calculation.
Calculation formula Rk,j depends on the distribution type:
Normal (Gauss) Distribution
Rk,j - pseudo-random normally distributed value with the average bj and the spread dj.
Student's Distribution
Rk,j - t-value of the Student's distribution with the random probability (0 to 1) and the degree of freedom equal to 2.
Chi-Square Distribution
Rk,j - pseudo-random chi-square distributed number with the degree of freedom equal to 1.
Bilateral Exponential Distribution
The following is calculated for each financial instrument included into yield matrix:
xj - the number of elements smaller than 0.
yj - the number of elements greater than 0.
zj - the number of elements equal to 0.
xj - mean of negative elements.
yj - mean of positive elements.
If means are ignored, zj is always assumed to be equal to zero.
Auxiliary values are calculated to generate the values Rk,j:
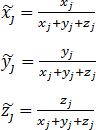
A random value t in the interval from 0 to 1 is generated for each k.
If 
, then Rk,j is exponential distribution with 
intensity.
If 
, then Rk,j is equal to zero, otherwise Rk,j is exponential distribution with 
intensity.
Weibull Distribution
Rk,j - pseudo-random variable that follows the Weibull distribution with the parameters dj and bj, namely, the value ,
where p is a pseudo-random variable uniformly distributed at the interval between 0 and 1.
Gamma Distribution
Rk,j - inverse gamma distribution with random probability p (from 0 to 1).
Uniform Distribution
Rk,j - random variable uniformly distributed between the beginning of the interval dj (inclusive) and the end of the interval dj (exclusive).
- means of financial instruments.
- standard deviations based on the sample of financial instruments.
If the Cholesky factorization is used, the H Cholesky matrix is generated based on the COR correlation matrix. Each row of the R matrix is multiplied by the Cholesky matrix following the rules of multiplication for a row vector and a matrix. The obtained vector replaces a row of the R matrix.
VaR is calculated using historical method, but the R generated matrix is used instead of yield matrix.
The output parameter is the matrix VaR = ǁVaRlǁ, that contains VaR of portfolio of each organization included into calculations.
See also: