– flow of the i-th industry production to be consumed by the j-th industry, intermediate consumption.The Input-output Balance model is used to study economy sectors, interindustry relationships, industry input and output, and price indicators.
Given below is an example of an input-output model:
| Industry | Agriculture | Services | Total | C | I | G | E | X | |
| Total | M1 | M2 | M3 | ƩM | ƩC | ƩI | ƩG | ƩE | ƩX |
| Industry | X11 | X12 | X13 | M1 | C1 | I1 | G1 | E1 | X1 |
| Agriculture | X21 | X22 | X23 | M2 | C2 | I2 | G2 | E2 | X2 |
| Services | X31 | X32 | X33 | M3 | C3 | I3 | G3 | E3 | X3 |
| D | D1 | D2 | D3 | ƩD | |||||
| W | W1 | W2 | W3 | ƩW | |||||
| P | P1 | P2 | P3 | ƩP | |||||
| T | T1 | T2 | T3 | ƩT | |||||
| Z | Z1 | Z2 | Z3 | ƩZ | |||||
| X | X1 | X2 | X3 | ƩX |
In tables of this model, the j-th column presents the j-th sector consumption of resources and products from other industrial sectors, the i-th row shows the i-th sector output by types of products.
An input-output model has 3 quadrants.
It shows intersectoral flows. – flow of the i-th industry production to be consumed by the j-th industry, intermediate consumption.
Therefore, it is available to calculate the volume of the produced output for intermediate consumption by summing up the 
values by the 
row. Total intermediate consumption for the economy:
It includes information on use and final consumption of GDP (GDP based on market prices). 
- household consumption, 
- gross investment, 
- government expenses, 
- net export. Summing up these values by sectors results in the appropriate values for economy as a whole:
, 
, 
, 
GDP calculated using expenditures method equals to 
.
Therefore, the 
vector, where 
, is the vector of end consumption of the sectors.
The III quadrant includes information on what GDP is made up of (GDP based on prices). The following information is available for each j-th sector:
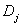. Depreciation.
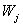. Salaries and wages.
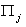. Income.
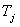. Taxes less state subsidies for real sector.
Summing up each of these components results in the appropriate value for the economy as a whole:
, 
, 
, 
In its turn, the sum of these components gives the value of GDP, calculated based on income: 
.
You can calculate GDP based on added values by sectors:
Given below is the balance expression showing i-th sector's products by types:
Given below is the balance expression showing j-th sector's consumption of materials, raw materials and resources:
Summing up the first expression by i and the second expression by j results in:
Thus, the total final output equals to the total net product.
The input-output model assumes directly proportional relationship between raw materials consumption 
by the industry j and its gross output 
. This proportionality coefficient 
is named the coefficient of direct costs and shows necessary expenditures of the product of industry i to produce a unit of industry j.
Matrix A is the matrix of coefficients of direct expenses 
.
Therefore, the expression can be rewritten as: 
.
Or in vector form: 
Where 
- the vector of gross output by sectors.
Thus, knowing the volumes of gross output for industries x and having the matrix of direct costs A, it is available to find the values of end consumption y in the following way: 
.
Where E - the unit matrix. This problem is named a direct problem.
When the volumes of end consumption are known and it is required to find sectors' output (reverse problem), the following equation should be used: 
.
See also:
Library of Methods and Models | Modeling Container: The Input-Output Balance Model