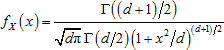
Student's Distribution

Student's distribution with d degrees of freedom is described by probability density function:

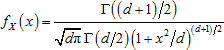
Where Г - gamma function that looks as follows:

The function implements an algorithm based on the following property: if a random variable Y follows standard normal distribution, and the variable Z follows χ2 distribution with d degrees of freedom, and if Y and Z are independent, the variable has Student's distribution with d degrees of freedom. As the χ2(d) distribution is a special case of gamma distribution and matches Г(d/2, 2), the gamma distribution function is used. Thus, the following operations are executed to generate pseudo-random value X ~ t(d):

1. Draw a sample Y ~ N(0,1) from standard normal distribution using the Box-Muller method (see description of normal distribution).

2. Using the gamma distribution function, generate a sample from the χ2 distribution with d degrees of freedom Z ~ χ2(d) = Г(d/2, 2). This sample must be independent from Y.

3. Calculate values of elements of required sample .