Value-At-Risk (VaR) is one of the most common forms of measuring financial risks. It is generally referred to as VaR. This indicator shows the amount of possible loss with a specified probability for a certain period of time.
The main point of VaR is a clear and definite answer to the question: what maximum loss may the investor incur for a certain period of time with a specified probability? This implies that the VaR value is defined as the largest expected loss the investor can incur with a specified probability during n days.
The key parameters of VaR are a period of time, for which the risk is calculated, and the specified probability that the loss does not exceed a certain amount. For example, the standard for the broker-dealer reports on transactions with off-market derivatives sent to the US Securities and Exchange Commission is a 2-week period and 99% probability. The Bank of International Settlements established the 99% probability and a 10-day period to assess the adequacy of bank capital. JP Morgan publishes its daily VaR values at the 95% confidence level.
VaR is a universal method for calculating various types of risk:
Price Risk. The risk of changes in the value of a financial asset price on the market.
Currency Risk. The risk associated with a change of the market exchange rate of the national currency against the currency of another country.
Credit Risk. The risk associated with a partial or complete failure of the borrower to repay a loan.
Liquidity Risk. The risk associated with the inability to sell a financial asset, or big losses incurred by selling the asset because of the big difference between the purchase and sale market value.
Two matrices are used as input parameters of the calculation:
Matrix with Financial Instruments. Includes the following dimensions:
Date. Consists of calculation date and dates included into retrospection period. This dimension must not contain any missing data, starting from calculation date and ending with the last date of the retrospection period.
Financial instruments.
Value.
Portfolio is a matrix that contains a list of organizations and the number of financial instruments used by the organizations. It includes the following dimensions:
Organization.
Financial instruments.
Value.
Before calculating the VaR model, it is required to calculate the following values:
Yield.
Correlation matrix.
Average values.
Standard deviation based on sample.
If missing data treatment is used, the financial instrument matrix is checked for empty values (Null). Each financial instrument is checked from the first retrospection date up to the calculation date. If a Null value occurs, it is replaced with the first non-empty value of the previous date of the retrospection period; if all values of the previous periods are empty, the value remains Null.
For each financial instrument we calculate yield at the calculation date and for the whole retrospection period, starting from a date, after the first date in the period, after the number of days selected as the time horizon. If logarithmic yield is used, the calculations are based on the following formula:
Otherwise, the following formula is used:
Where:
. The price of the j-th financial instrument at the i date.
i = h, h+1, … N. Date in the calculation period:
i = 1. The latest date in the period.
i = h + 1. The date that comes after h days after the first date in the period.
N. Calculation date.
h. The value of time horizon.
j = 1, 2, … M. The number of selected elements in the financial instrument dimension of the financial instrument matrix.
For all financial instruments: 
Correlation matrix is calculated based on the obtained yield matrix. If the zero mean hypothesis is not used, the mean is calculated for the whole period of selected dates for each financial instrument (empty values are ignored):
Where:
ai,j. The yield of the j-th financial instrument at the i date.
Sj. The number of non-empty yield values for the j-th financial instrument.
Aj. Average value of the selected period for the j-th financial instrument.
Then, subtract the vector of means from each row of the yield matrix according to the rules of matrix subtraction:
Where Li - a row of the yield matrix:
Yield matrix:
To calculate correlation matrix, the covariance matrix is calculated by the following formula:
Where:
λ = 0.9.
C. Covariance matrix.
Correlation matrix is calculated by the formula:
Where:
t, k. Covariance matrix size.
. Correlation matrix.
Mean (empty values are ignored) and standard deviation based on sample are calculated for each financial instrument. Yield matrix is used as the data source.
. Average values of financial instruments.
. Standard deviations based on financial instrument sample.
M. The number of selected elements in the financial instrument dimension of the financial instrument matrix.
Formula to calculate standard deviation based on sample:
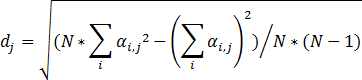
Where i = 1, 2, … N is the number of selected elements in the dates dimension of the financial instrument matrix. i = 1 corresponds to the latest date of the period, while N corresponds to the calculation date.
VaR is estimated in three ways:
See also:
Library of Methods and Models | Back-Testing: Traffic Lights Principle | Modeling Container: The Value-At-Risk Model