Delta-Normal Calculation Method

The method is used to calculate the VaR model.

Calculation is executed for each organization and for each instrument of the organization portfolio.

If the random-walk hypothesis is used, the horizon coefficient is calculated by the formula: . If the hypothesis is not used:

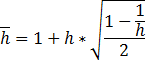
Where h - horizon coefficient, h - value of time horizon parameter.

Then calculate the q quantile of the level 1 - α of normal distribution. Where α - the value of significance level (available values lie within the range from 0 to 1).

If the zero mean hypothesis is not used, the auxiliary parameter qj = q.

If the zero mean hypothesis is used, if the value of this tool from the briefcase is negative and long and short positions differ, q is calculated by the following formula: qj = q + bj. In other cases the formula looks as follows: qj = q - bj. Where bj - the average value of the j-th financial instrument.

Then calculate volatility for each of the instruments:

Where dj - standard deviation based on a sample of the j-th financial instrument.

If logarithmic yield is used, the VaR is calculated as:

If logarithmic yield is not used:

Where:

pl,j. The quantity of the j-th financial instrument in the portfolio of the l-th organization.
ν1,j. Price of the j-th financial instrument at the calculation date.

Portfolio VaR is calculated for each organization. To do this, VaR vector for financial instruments of each organization is multiplied by the COR correlation matrix:

The output vector is scalarly multiplied by VaR vector for financial instruments:

Take square root of the obtained value:

Where VaRl - VaR of the portfolio of the l-th organization.

The output parameter is the matrix VaR = ǁVaRlǁ that contains VaR of portfolio of each organization included into calculations.