Value-At-Risk (рисковая стоимость) - одна из самых распространенных форм измерения финансовых рисков. Общепринято обозначается «VaR». Этот показатель характеризует величину возможного убытка с выбранной вероятностью за определенный промежуток времени.
Сутью VaR является четкий и однозначный ответ на вопрос: какой максимальный убыток рискует понести инвестор за определенный период времени с заданной вероятностью? Отсюда следует, что величина VaR определяется как наибольший ожидаемый убыток, который с заданной вероятностью может получить инвестор в течение n дней.
Ключевыми параметрами VaR является период времени, на который производится расчет риска, и заданная вероятность того, что потери не превысят определенной величины. Например, стандартом для брокерско-дилерских отчетов по операциям с внебиржевыми производными инструментами, передаваемым в Комиссию по биржам и ценным бумагам США, являются 2-недельный период и 99%-вероятность. The Bank of International Settlements для оценки достаточности банковского капитала установил вероятность на уровне 99% и период, равный 10 дням. JP Morgan опубликовывает свои дневные значения VaR при 95% доверительном уровне.
VaR является универсальной методикой расчета различных видов риска:
ценового риска. Риск изменения стоимости цены финансового актива на рынке;
валютного риска. Риск, связанный с изменением рыночного валютного курса национальной валюты к валюте другой страны;
кредитного риска. Риск, возникающий при частичной или полной неплатежеспособности заемщика по взятому кредиту;
риска ликвидности. Риск, связанный с невозможностью продажи финансового актива, либо с большими убытками, возникающими при продаже актива в силу большой разницы величины покупки/продажи, существующей на рынке.
При расчете на вход подаются две матрицы:
матрица с финансовыми инструментами. Состоит из измерений:
дата. Включает дату расчета и даты, входящие в период ретроспективы. Измерение не должно содержать пропусков, начиная от расчетной даты и заканчивая последней датой из ретроспективы;
финансовые инструменты;
значение.
портфель - матрица, содержащая список организаций и количество финансовых инструментов, которые имеются у организаций. Состоит из измерений:
организации;
финансовые инструменты;
значение.
Перед расчетом VaR необходимо рассчитать следующие величины:
доходность;
матрицу корреляций;
средние значения;
стандартные отклонения по выборке.
Если используется заполнение пропусков, то производится проверка матрицы финансовых инструментов на наличие пустых значений (Null). Проверка проводится с первой даты ретроспективы до расчетной даты по каждому финансовому инструменту. Если встречается значение Null, то вместо него устанавливается первое непустое значение за предыдущую дату, входящую в период ретроспективы, если за предыдущие периоды все значения являются пустыми, то значение остается пустым.
Для каждого финансового инструмента производится расчет доходности на расчетную дату и на весь период ретроспективы, начиная с даты после первой даты в периоде, через количество дней, указанных в качестве временного горизонта. Если используется логарифмическая доходность, то расчет производится по формуле:
![]()
Если логарифмическая доходность не используется, то по формуле:
![]()
Где:
![]() . Стоимость j-го
финансового инструмента на i
дату;
. Стоимость j-го
финансового инструмента на i
дату;
i = h, h+1, … N. Дата в расчетном периоде:
i = 1. Самая младшая дата в периоде;
i = h + 1. Дата, наступающая через h дней после первой даты в периоде;
N. Расчетная дата;
h. Значение временного горизонта;
j = 1, 2, … M. Количество выделенных элементов в измерении финансовых инструментов (матрица финансовых инструментов).
Для всех финансовых инструментов: ![]()
На основе полученной матрицы доходности считается матрица корреляций. Если не используется гипотеза о нулевом среднем, то считается среднее значение за весь период отмеченных дат для каждого финансового инструмента (пустые значения не учитываются):
![]()
Где:
ai,j. Доходность j-го финансового инструмента на i дату;
Sj. Количество непустых значений доходности для j-го финансового инструмента;
Aj. Среднее значение за весь период отмеченных дат для j-го финансового инструмента.
Далее из каждой строки матрицы доходности вычитается вектор средних значений, по правилам вычитания матриц:
![]()
Где Li - строка из матрицы доходностей:
![]()
Матрица доходностей:

Для расчета матрицы корреляций считается матрица ковариаций по формуле:
![]()
![]()
Где:
λ = 0.9;
C. Матрица ковариаций.
Матрица корреляции считается по формуле:
![]()
Где:
t, k. Размер матрицы ковариаций;
![]() . Матрица корреляций.
. Матрица корреляций.
Для каждого финансового инструмента рассчитывается среднее значение (пустые значения не учитываются) и стандартное отклонение по выборке. Источником данных является матрица доходности.
![]() . Средние значения финансовых инструментов.
. Средние значения финансовых инструментов.
![]() . Стандартные отклонения по выборке финансовых
инструментов.
. Стандартные отклонения по выборке финансовых
инструментов.
M. Количество выделенных элементов в измерении финансовые инструменты матрицы финансовых инструментов.
Формула расчета стандартного отклонения по выборке:
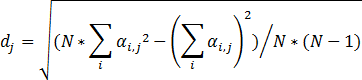
Где i = 1, 2, … N - количество выделенных элементов в измерении даты (матрица финансовых инструментов). i = 1 соответствует самой младшей дате в периоде, N соответствует расчетной дате.
Расчет VaR производится тремя методами:
См. также:
Библиотека методов и моделей | Бэктестинг: «Принцип светофора» | Контейнер моделирования: модель «Value-At-Risk»