Метод используется для расчёта модели VaR.
Расчёт проводится для каждой организации по каждому инструменту из портфеля организации.
Если используется гипотеза о случайном блуждании, то коэффициент горизонта рассчитывается по формуле: ![]() . Если гипотеза не используется:
. Если гипотеза не используется:
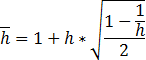
Где h - коэффициент горизонта, h - значение параметра временного горизонта.
Далее считается квантиль q уровня 1 - α нормального распределения. Где α - значение уровня значимости (допустимые значения от 0 до 1).
Если гипотеза о нулевом среднем не используется, то вспомогательный параметр qj = q.
Если используется гипотеза о нулевом среднем, то при условии, что значение данного инструмента из портфеля отрицательное и различаются длинные и короткие позиции, то q считается по формуле: qj = q + bj. В других случаях формула имеет вид: qj = q - bj. Где bj - среднее значение j-го финансового инструмента.
Далее для каждого инструмента считается волатильность:
![]() .
.
Где dj - стандартное отклонение по выборке j-го финансового инструмента.
Если используется логарифмическая доходность, то VaR рассчитывается по формуле:
![]() .
.
Если логарифмическая доходность не используется:
![]() .
.
Где:
pl,j. Количество j-го финансового инструмента из портфеля l-ой организации;
ν1,j. Стоимость j-го финансового инструмента на дату расчета.
Для каждой организации рассчитывается VaR портфеля. Для этого вектор VaR по финансовым инструментам каждой организации умножается на матрицу корреляций COR:
![]()
Полученный вектор скалярно умножается на вектор VaR по финансовым инструментам:
![]()
Из полученного числа извлекается квадратный корень:
![]()
Где VaRl является VaR портфеля l-ой организации.
Выходным параметром является матрица VaR = ǁVaRlǁ, содержащая VaR портфеля каждой организации, участвующей в расчете.
См. также: