Метод главных компонент (англ. Principal component analysis, PCA) - один из основных методов, используемых для уменьшения размерности данных с наименьшей потерей информации. Разработан К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется в распознавании образов, сжатии данных, компьютерном зрении и т. п. Вычисление главных компонент сводится к расчёту собственных векторов и собственных значений матрицы исходных данных. Также метод главных компонент известен как преобразование Кархунена-Лоэва (англ. Karhunen-Loeve) или преобразование Хотеллинга (англ. Hotelling transform).
Пусть Х(n x m) - матрица наблюдений за переменными x1, x2, …, xm и пусть S - матрица этих переменных. Варианты расчёта матрицы S в зависимости от её типа:
матрица корреляций:
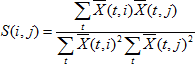
стандартизованная матрица:
![]()
матрица сумм квадратов и перекрестных произведений:
![]()
матрица вариаций-ковариаций (используется в большинстве случаев):
![]()
Вектор a1 размерности ![]() находится из условия:
находится из условия:
![]()
При ограничении:
![]()
Переменная ![]() называется первой главной компонентой, дает такую линейную комбинацию z1 переменных x1, x2, …, xm, которая максимизирует дисперсию.
называется первой главной компонентой, дает такую линейную комбинацию z1 переменных x1, x2, …, xm, которая максимизирует дисперсию.
Вторая и последующие главные компоненты:
![]()
Находится из условий:
![]()
В этом случае aj - собственные вектора матрицы S.
См. также:
Библиотека методов и моделей | ISmPrincipalComponentAnalysis