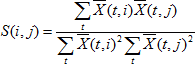
The principal component analysis (PCA)) is one of the key methods that are used to reduce data dimension while losing the least information. Invented by Karl Pearson in 1901. It is used in pattern recognition, data compression, computer vision, and so on. The calculation of principal components is reduced to the calculation of eigenvectors and eigenvalues of the original data matrix. Sometimes the PCA is named as Karhunen-Loeve transform) or Hotelling transform).
Assume that X(n x m) is a matrix of observations of the x1, x2, …, xm variables, and S is the matrix of these variables. The S matrix is calculated depending on its type:
Correlation matrix:
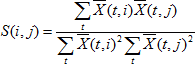
Standardized matrix:
Matrix consisting of sums of squares and cross-products:
Variance-covariance matrix (used in most cases):
The a1 vector of the 
dimension is derived from the condition:
Under the constraint:
The 
variable is named the first principal component. It produces such a linear combination z1 of the x1, x2, …, xm variables , that maximizes the variance.
The second and the following principal components:
Found based on the conditions:
In this case aj - eigenvectors of the S matrix.
See also:
Library of Methods and Models | ISmPrincipalComponentAnalysis