Hierarchical cluster analysis is a method of dividing a set of multidimensional objects into homogenous groups. This is an agglomerative method. Agglomerative methods consistently merge objects into clusters.
Initial data:
n. Number of objects.
m. Number of characteristics.
X. Objects' matrix.
Q. Required number of clusters.
Let X(n x m) be the matrix that describes n objects in Rm. Hierarchical clustering consecutively merges clusters with minimum distance between cluster, starting from n trivial clusters with one object in each cluster, and finishing at the step n - Q after forming exactly Q clusters.
Initially, the distances between one-object clusters are the distances between respective objects. At each step the user needs only to recalculate the distance between the newly merged cluster and the other clusters.
The inter-cluster distance, and, respectively, the method of recalculating the inter-cluster distance between an arbitrary cluster i and the cluster formed by merging j, k, can be defined in one of the following ways:
Nearest neighbor:
![]()
Maximum distance:
![]()
Group mean:
![]()
Centroid:
![]()
Median:
![]()
Minimum variation:
![]()
Where ni, nj, nk - cluster sizes.
The methods used to define initial inter-object distances:
Sum of modules:
![]()
Euclidean norm:
![]()
Root of Euclidean norm:
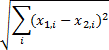
See also:
Library of Methods and Models | ISmHierarchicalClusterAnalysis