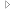 Example of problem solved using linear optimization
Example of problem solved using linear optimizationA linear optimization block is used to solve a problem of optimal use of limited resources.
In the problem controlling variables are resources, and criterion function is an entity that is subject to optimization. Problem solution is finding such values of controlling variables that satisfy the specified constraints and at which criterion function takes the maximum or the minimum value. Conditions, for which the problem is created, may change. To take into account these conditions without creating a new problem, criterion function coefficients are used that enable the user to account for influence of conditions change on criterion function calculation.
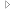 Example of problem solved using linear optimization
Example of problem solved using linear optimization
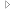 Create a new linear optimization block
Create a new linear optimization block
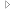 Edit ready linear optimization block
Edit ready linear optimization block
Creating and editing is executed using the linear optimization block editing wizard , which is used to set up block parameters.
Setting up linear optimization block includes the following steps:
It is assumed that a meat trading company owns warehouses situated in different Moscow districts. It is required to calculate the optimal number of products to be stored in each warehouse taking into account:
Company transportation expenses. They are specified using criterion function coefficients.
Amount of product in warehouses. It is specified by entering initial values of controlling variables.
Demand for each product type. It is specified using simple constraints of controlling variables.
Maximum warehouse capacity. It is specified using complex constraints of controlling variables.
Product storage unit is a box that is why integer variables are used.
In the example all data is entered by pasting from clipboard. It is done to speed up data entry in the example. When real linear optimization blocks are created, data is entered using keyboard.
See also: