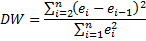
Тест Дарбина-Уотсона

Тест Дарбина-Уотсона используется для проверки гипотезы об отсутствии автокорреляции первого порядка в векторе остатков регрессионной модели.

Пусть (e1,…,en) - это вектор остатков линейной регрессии по k независимым переменным (включая константу). Предполагая, что остатки образуют авторегрессионный процесс первого порядка, можно описать их связь рекуррентным соотношением et = ρet-1 + υt, где υt – последовательность независимых случайных величин с нормальным распределением.

Тест основан на проверке гипотезы об отсутствии автокорреляции H0: ρ = 0, критерием служит статистика Дарбина-Уотсона, которая рассчитывается по следующей формуле:

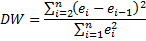
Можно доказать, что DW ≈ 2*(1- r), где r - коэффициент корреляции между ei и ei-1. Таким образом, значения DW находятся в промежутке от 0 до 4. В случае отсутствия автокорреляции DW близка к 2. Близость к 0 говорит о положительной автокорреляции, к 4 - об отрицательной.

На практике проверка гипотезы H0 об отсутствии автокорреляции остатков осуществляется с помощью сравнения статистики DW с теоретическими значениями dl и du для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости α:

0 < DW < dl - гипотеза H0 отвергается, есть положительная автокорреляция;
dl < DW < du - зона неопределённости;
du < DW < 4 - du - гипотеза H0 не отвергается, автокорреляции нет;
4 - du < DW < 4 - dl - зона неопределённости;
4 - dl < DW < 4 - гипотеза H0 отвергается, есть отрицательная автокорреляция.

Численные методы позволяют вычислить уровень значимости, при котором значение DW будет совпадать со значениями dl и du. Полученные таким способом pl и pu можно интерпретировать следующим образом:

pl ≤ α – гипотеза H0 отвергается, есть автокорреляция (положительная, если DW < 2, отрицательная, если DW > 2);
pl > α, pu ≤ α – зона неопределённости;
pu > α – гипотеза H0 не отвергается, автокорреляции нет.

См. также: