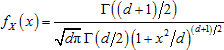
Распределение Стьюдента с количеством степеней свободы d характеризуется функцией плотности вероятности:
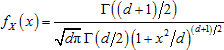
Где Г - гамма-функция, имеющая вид:
![]()
В функции реализован алгоритм, основанный на том свойстве, что если случайная величина Y имеет стандартное нормальное распределение, величина Z имеет χ2-распределение с d степенями свободы, и при этом если Y и Z являются независимыми, то величина ![]() имеет распределение Стьюдента с d степенями свободы. Поскольку распределение χ2(d) является частным случаем гамма-распределения и совпадает с Г(d/2, 2), то используется функция гамма-распределения. Таким образом, для генерирования псевдослучайной величины X ~ t(d) выполняются следующие операции:
имеет распределение Стьюдента с d степенями свободы. Поскольку распределение χ2(d) является частным случаем гамма-распределения и совпадает с Г(d/2, 2), то используется функция гамма-распределения. Таким образом, для генерирования псевдослучайной величины X ~ t(d) выполняются следующие операции:
1. Генерируется выборка Y ~ N(0,1) из стандартного нормального распределения при помощи метода Бокса-Мюллера (см. описание нормального распределения).
2. При помощи функции гамма-распределения генерируется независимая от Y выборка из χ2-распределения с d степенями свободы Z ~ χ2(d) = Г(d/2, 2).
3. Вычисляются значения элементов искомой выборки ![]() .
.
См. также: