Durbin-Watson Test

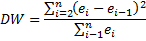
The Durbin-Watson test is used to check hypothesis about absence of the first-order correlation in regressions model residuals vector.

Let (e1,…,en) be a linear regression residuals vector by k independent variables (including constant). Suppose that residuals form first-order autoregression, their relation can be described by recurrent correlation et = ρet-1 + υt, where υt is a sequence of independent random values with normal distribution.

The test is based on checking the hypothesis of absence of autocorrelation H0: ρ = 0, the Durbin-Watson statistic is a criterion and it is calculated according to the following formula:

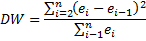
It can be proved that DW ≈ 2*(1- r), where r is a correlation coefficient between ei and ei-1. Thus, the DW are between 0 and 4. In case of autocorrelation absence, DW is close to 2. Closeness to 0 means positive autocorrelation, to 4 - about negative autocorrelation.

In practice, the H0 hypothesis about residuals autocorrelation is checked by comparing the DW statistics with theoretical values dl and du for the specified number of observations n, the number of independent variables of model k and the significance level α:

0 < DW < dl - the H0 hypothesis is rejected, there is positive autocorrelation.
dl < DW < du - ambiguity area.
du < DW < 4 - du - the H0 hypothesis is not rejected, there is no autocorrelation.
4 - du < DW < 4 - dl - ambiguity area.
4 - dl < DW < 4 - the H0 hypothesis is rejected, there is negative autocorrelation.

Numeric methods enable the user to calculate significance level, at which value of DW matches with values of dl and du. pl and pu obtained by this method can be interpreted as follows:

pl ≤ α – the H0 hypothesis is rejected, there is autocorrelation (positive if DW & lt; 2, negative if span style="font-style: italic;">DW & gt; 2).
pl > α, pu ≤ α – ambiguity area.
pu > α – the H0 hypothesis is not rejected, there is no autocorrelation.