Initial system:
The following methods are usually used to solve a system of non-linear equations:
Hybrid Method. To solve the initial system, a modification of a hybrid algorithm implemented in the mathematical methods library MINPACK-1, is used.
Minimum of Errors. Find minimum of the function that has n variables:
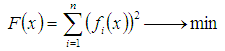
Newton Method. The initial system is solved using iterations by calculating partial derivatives:
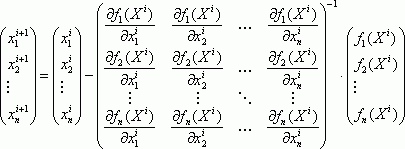
Where:
Initial value:
- 
Value 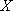for a new iteration:
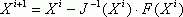
Partial derivative:
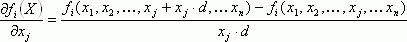
d. Relative increment of argument.
Iterations continue until the specified number of iterations is completed or the required accuracy of the solution is achieved.
Modified Method of Simple Iterations. A set of initial values is specified for each variable. At each iteration, the values of this set are substituted to each equation of the system Fi(xi). Values of the set that have already been calculated during the current iteration are substituted in the new form:
This method differs from the non-modified simple iteration method in the following way: input values at each iteration are fully taken from the previous iteration, that is, already calculated values are not used at the current iteration.
Iterations continue till deviation of the obtained results from the last iteration results by a selected norm will not exceed the specified value.
See also:
Library of Methods and Models | Modeling Container: The System of Non-Linear Equations Model | ISmNonLinearEquations