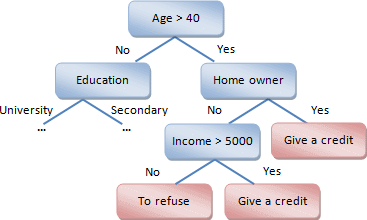
Decision Tree

Decision trees are a way of presenting rules in a hierarchical and sequential structure where for each object there is one node with a decision.

A rule is an "If... then" logical structure. For example:

The tree consists of internal nodes that contain test conditions and leaves that are decisions.

Building a Decision Tree

Suppose there is a set T that contains objects, each of which is characterized by m attributes, and one of the attributes indicates that an object belongs to a certain class.

Consider the idea of building decision trees from a set T (first developed by Hunt) according to R. Quinlan).

Let denote classes via {C₁, C₂, … C_k}, then the following situations are possible:

The set T contains one or more objects related to one C_k class. Then the decision tree for T is a leaf that defines the C_k class.
The T set does not contain any examples, so it is an empty set. Then it is a leaf again, and the class associated with the lead is selected from a different set than T, for example, from a set associated with the parent.
The T set contains objects related to different classes. In this case, partition the T sets to subsets. To do this, select one of the attributes that has two and more distinct values: O₁, O₂, … O_n. T is divided into subsets T₁, T₂, … T_n, where each T_i subset contains all objects that have the value O_i for the selected attribute. This procedure recursively continues until the finite set consists of objects related to the same class.

The above described procedure is the basis for many modern algorithms for building decision trees. This method is also known as divide and conquer. Using this method, a decision tree is built from top to bottom.

Since all the objects have been previously assigned to the known classes, this process of building a decision tree is named supervised learning. The learning process is also named inductive learning or tree induction.