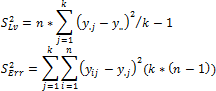
Analysis of variance (ANOVA) is used to examine how one or several qualitative variables (factors) affect one dependent quantitative variable.
Single-factor analysis of variance tests the hypothesis on equality of the means of several general populations. For example, if it is required to find out whether the input dependent variable x affects the output dependent variable y. In this example the input variable x has discrete values, while the output variable y is a continuous random value with the probabilistic nature caused by the presence of the additive noise e.
Single-factor analysis of variance is based on the following assumptions:
In each observation, ei has a normal distribution with the zero mean and finite variance.
For each i the variance ei is a constant.
Consider a procedure of calculating single-factor analysis of variance. Let x take k various values, or, in other words, the factor x has k levels. Let there be n observations of the output value y at each level. Then the results can be shown as a table where the columns are levels of the factor x, and the rows are observations of y):
| № of observation | Levels of the input factor x | ||||
| 1 | 2 | … | j | … | |
| 1 | y11 | y12 | … | y1j | … |
| 2 | y21 | y22 | … | y2j | … |
| … | … | … | … | … | … |
| i | yi1 | yi2 | … | yij | … |
| … | … | … | … | … | … |
| n | yn1 | yn2 | … | ynj | … |
If levels of the x factor do not affect the mean for y, all the observations are a sample of the same general population (provided that the conditions listed above are satisfied). Then the variance of the general population can be estimated in two independent ways: using average values y for each of the levels x, or as arithmetic mean of the estimates of variances y for each of the levels x. The first estimate is known as the estimate of variance for the levels S2Lv, the second one estimates error variance S2Err.
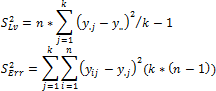
Where:
y.j. Mean of the j-th level.
y... Common mean.
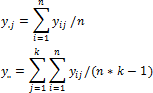
If the levels of the x factor do not affect the mean, the ratio F = S2Lv/S2Err follows the Fisher distribution rule. Characteristics of this distribution depend on the number of degrees of freedom for the estimates S2Lv and S2Err (number of degrees of freedom for the numerator ν1=(k-1) and the denominator ν2=k*(n-1)). For each specified significance level α there is always such a critical value Fcrit, that can be exceeded by F (if the levels x do not affect it) with the probability not greater than α. This means that if after the data calculation the calculated value of F statistics exceeds corresponding Fcrit, the data contradicts the hypothesis on the equality of means y for all levels of x. If F<Fcrit, the data does not contradict the hypothesis, and the levels of x are assumed to not affect the mean for y.
Two-factor analysis of variance tests the hypothesis on the equality of the means of the controlled output parameter y with various levels of the two factors.
In this model x1 and x2 input variables have distinct states and y output variable is continuous random value, the likelihood nature of which is based on the existence ofe additive noise.
Two-factor analysis of variance is based on the following assumptions:
In each observation, ei has a normal distribution with the zero mean and finite variance.
For each i the variance ei is a constant.
Consider a procedure of two-factor analysis of variance. Suppose x1 takes k different values or x1 factor has k levels, x2 takes m different values of x2 factor has m levels. Let there be n observations of the output variable y at each of the level combinations. Then the results can be displayed as the following table:
| Levels of the input factor x2 | Levels of the input factor x1 | ||||
| 1 | 2 | … | j | … | |
| 1 | y111 … y11n | y121 … y12n | … | y1j1 … y1jn | … |
| 2 | y211 … y21n | y221 … y22n | … | y2j1 … y2jn | … |
| … | … | … | … | … | … |
| i | yi11 … yi1n | yi21 … yi2n | … | yij1 … yijn | … |
| … | … | … | … | … | … |
| m | ym11 … ym1n | ym21 … ym2n | … | ymj1 … ymjn | … |
If the levels of factors x1 and x2 do not affect the y mean, all observations are the sample from the same general population (provided that the assumptions listed above are satisfied). Then the variance of the general population can be estimated in the following independent ways: using average values y for each of the factor levelsx1 or x2, or as the arithmetic mean of the estimates of variances x for each of the levels x1 or x2. As in single-factor analysis of variance, the first estimate is named the estimate of variance of the levels S2Lv, the second one is named the estimate of the error variance S2Err.
For the first and the second factor:
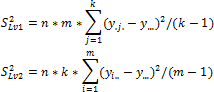
Where:
y.j.. Mean by j-th level of the first factor.
yi... Mean by i-th level of the second factor.
y.... Common mean.
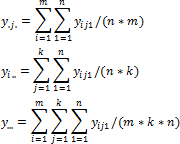
The estimate of error variance is calculated as follows:
![]()
Where:
yij.. The mean value y at j-th level of the first factor and i-th level of the second factor.
Two factors enable the use of one more variance estimate, that is, the interaction:
![]()
If there is no influence of levels of factors x1 and x2 on the mean, relations F1=S2Lv1/S2Err, F2=S2Lv2/S2Err and FInt=S2Int/S2Err follow the rule of Fisher distribution. Characteristics of this distribution depend on the number of degrees of freedom of the estimates S2Lv1, S2Lv2, S2Int and S2Err (number of degrees of freedom for the numerator ν1=(k-1), ν2=(m-1), νInt=(m-1)*(k-1) and the denominator νErr=m*k*(n-1) ). For any specified significance level α there is also a critical value Fcrit, which can be exceeded by F with no influence of factor levels x1, x2 and their interaction x1*x2 with likelihood not greater than α. This means that if after the data calculation the calculated value of F statistic exceeds the corresponding Fcrit, the data contradicts the hypothesis on the equal y means for all factor levels x1, x2 and their mutual effectx1*x2. If F<Fcrit, then the data does not contradict this hypothesis and it is considered that levels do not influence the y mean.
See also: