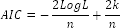
Information criteria are used to compare models with different number of parameters, when it is necessary to select the best set of explanatory variables. These criteria take into account the number of n observations and the number of p model parameters and differ from each other with the penalty function type for the number of parameters. All criteria are calculated based on the LogL log-likelihood function that enables the use of it for a wide range of models.
The following rule is applicable for information criteria: the best model has the least criterion value.
The criterion is calculated by the formula:
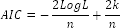
In contrast to the Akaike criterion, the Schwarz criterion imposes a big "penalty" for additional parameter use:
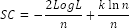
This criterion is a one more alternative for the Akaike and Schwarz criteria:
See also:
Library of Methods and Models | ISummaryStatistics.AIC | ISummaryStatistics.SC | ISummaryStatistics.HQcriterion