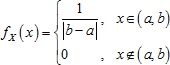
Continuous uniform distribution at the interval (0, 1) is described with probability density function fX(x) = 1 at (0,1); fX(x) = 0 outside (0,1).
Continuous uniform distribution at the interval (a, b) is described with probability density function:
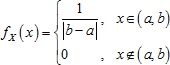
The function calculates values xi = a + (b − a)vi (on condition that a < b), with the sample of pseudo-random values v1, …, vn is generated from a standard uniform distribution at the interval (0, 1). It is assumed that the values x1, …, xn belong to the interval (a, b).
See also:
ISmUniformDistribution | Library of Methods and Models