Multivariate Normal Distribution

Density function of multivariate normal distribution for each vector x in d-dimensional space is determined as:

Where:

μ = (μ1, μ2, …, μd)T. Vector of means.
Σ. Covariance matrix with (i, j)-th element Σij = Cov(Xi, Xj). That is why Σ is symmetric positive-definite.
|Σ|. Determinant of matrix Σ.
Σ-1. Matrix inverse to Σ.

As the Σ matrix is symmetric positive-definite, it can be expanded into factors Σ = CCT (Cholesky decomposition), when the C matrix with the number of rows and columns d×d is the lower triangle. Accepting that cij is the (i, j)-th element of the C matrix, the algorithm that is used to generate required vector X with multivariate normal distribution looks as follows:

Execute the Cholesky decomposition for the Σ matrix to find the C matrix, which satisfies the requirement that Σ = CCT, is lower triangular and contains strictly positive diagonal entries:

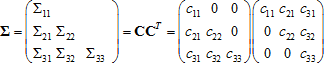
Elements of the C matrix are calculated as follows:

with j < i:

Generate the Z1, Z2, …, Zd samples from independent and similarly distributed values with the N(0, 1) distribution, each sample contains by n elements. Box-Muller method is used (see description of normal distribution).
Accept for i = 1, 2, …, d:

The X = (X1, X2, …, Xd)T value is returned. In matrix form X = μ + CZ.