Hypergeometric Distribution

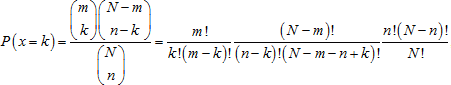
The hypergeometric distribution models the number of successes during sample from a finite population without replacement. If a random value X corresponds to hypergeometric distribution, the probability of getting exactly k successes in a sample containing n elements is described by the following formula:

If k = max(0, m + n – N) ,… , min(n, m), then

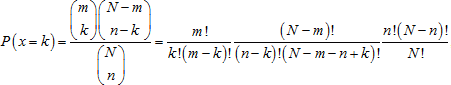
Otherwise P(x = k) = 0

Where:

N. Population volume.
n. Sample volume.
m. The number of "successful" elements in the N population.

Random values are generated using an algorithm (described by Fishman, 1978) based on inverse transform method. Algorithm is based on a recursive formula:

Starting with:

When n < N - m:

When n < N - m:

Thus, to generate a sample from hypergeometric distribution, we use an algorithm, which includes the following steps:

If n < N - m, assume that:

xi = 0

Otherwise:

xi = n – N + m

Generate pseudo-random number ui ~ U(0, 1) distributed according to continuous uniform distribution at the interval (0, 1), when i = 1 … ns.
If ui ≤ p, the value xi is returned. Otherwise the previous three steps are repeated until the condition ui ≤ p is fulfilled:

xi = xi + 1

ui = ui – p

then the value xi is returned.

Steps 2 and 3 are executed ns times, each returned x value is one of the elements of the required sample.