Density of beta distribution with parameters α, β at the point x is determined by the following equation:
![]()
Where full beta function:
![]()
Thus, the value of integral beta distribution function:
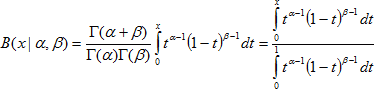
If distribution is defined not for a standard range [0, 1] (actual range of a random value), and for a random range [A, B] , the general distribution function is reduced to standard by simple scaling, and looks as follows:
![]()
To calculate the value of integral beta distribution function, it is expanded to continued fraction:
![]()
Where:
![]()
![]()
Consider a sequence of even convergents showing a fairly good convergence under condition:
![]()
Otherwise:
![]() .
.
See also:
IStatistics.BetaDist | IStatistics.BetaInv | Library of Methods and Models