Quantile regression is a procedure of estimation of parameters of linear dependency between explanatory variables and specified level of explanatory value quantile. Unlike the ordinary least-squares method, quantile regression is a non-parametric method. It enables the user to get more information: regression parameters for any quantiles of dependent variable distribution. Moreover, such model is significantly less sensitive to outliers in data and to violations of hypothesis about distributions character.
Assume that Y is a random variable with function of distributing probabilities F(y) = Prob(Y ≤ y). Then the quantile of the τ level, where 0 < τ <1, is the least value Y, satisfying the condition F(y) > τ:
Q(τ) = inf{y:F(y) ≥ τ}
Considering the set of n observations by Y variable, traditional empirical distribution function is determined by the following formula:
Where I(Yi < y) function indicator, which gives 1, if the argument is TRUE and 0, if the argument is FALSE.
Appropriate empirical quantile is determined by the following formula:
Qn(τ) = inf{y:Fn(y) ≥ τ}
Record as the optimization problem is equivalent:
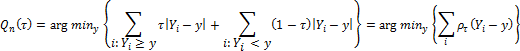
Where ρτ(u) = u(τ - I(u < 0)) is the function that weights positive and negative values of Yi - y in the different ways.
Quantile regression extends this problem, allowing to consider regressors.
Assume that conditional quantiles of specified values of the Y variable linearly depend on vector of explanatory variables X:
Q(τ|Xi,β(τ)) = X̕i,β(τ)
Where β(τ) is the vector of coefficients corresponding with τ quantile. Then the problem of unconditional minimization looks as follows:
This problem is solved using the modified simplex method.
One of the variants of observations sparsity estimation:
s(τ) = X*'(β(τ + h) - β(τ - h))/(2h), where:
where:
τ. Quantile.
X*. Vector of explanatory variables values.
h. Surroundings, for which the observations sparsity is calculated.
In the simplest case: X* = X̅ is a vector of average values of explanatory variables.
h is calculated by the following formula:
,
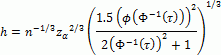Where zα = Φ-1(1 - α/2), α - a significance level.
For exact calculation of matrix, the value of observations sparsity is required. It is not required on approximate estimation.
To calculate ordinary covariance use the IIDRV (Independent and Identically Distributed Random Values, Ordinary(IID) covariance) the following formula is used:
cov(β) = s2(X'X)-1,
Where s2 = τ(1 - τ)s(τ)2 - error variance.
For calculation it is necessary to calculate quantile regression of the y = c type, where c - constant. Minimum value of criterion function is a required value.
For calculation it is necessary to calculate quantile regression described above.
For calculation it is necessary to calculate quantile regression of the y = c type, where c - constant. Estimated coefficient of the model is the required value.
It is calculated by the formula:
Pseudo R2 = 1 - objective/restr.objective,
where:
objective. Value of criterion function of specified model.
restr.objective. Value of restricted criterion function.
It is calculated by the formula:
,
where:
n. Number of observations.
k. Number of model coefficients, including a constant.
See also:
Library of Methods and Models | ISmQuantileRegression