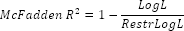
Due to the binary choice model features, model quality is estimated by statistics that are different from determination coefficient and Fisher statistics for regression model.
The RestrLogL restricted log-likelihood function is a value of the maximum likelihood function logarithm of restricted model (model where all factors are excluded). It is used to build McFadden determination coefficient and LR statistics.
Mean of log-likelihood function is calculated by the formula:
LogL/T
Where:
LogL. The maximum likelihood function logarithm value of calculated model.
T. Number of observations.
McFadden determination coefficient is identical to standard determination coefficient and is applied to estimate the quality of binary choice models.
McFadden determination coefficient is calculated by the formula:
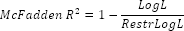
Where:
LogL. The maximum likelihood function logarithm value of calculated model.
RestLogL. Restricted log-likelihood function.
LR statistics is an analog of Fisher statistics and verifies hypothesis about insignificance of all model factors. It is calculated by the formula:
LR = -2(RestLog - LogL)
Where:
LogL. The maximum likelihood function logarithm value of calculated model.
RestLogL. Restricted log-likelihood function.
Statistics has a Chi-Squared distribution X2(k-1) where k is a number of regression factors without constant. The null hypothesis on the coefficients equality to zero for all regressors is rejected if the probability is less than the significance level. One of standard significance levels (0.1, 0.05 or 0.01) is considered.
It is calculated only if model has constant.
See also:
Library of Methods and Models | Adjusted Determination Coefficient | ISummaryStatistics.McFaddenRsquared | ISummaryStatistics.AvgLogL | ISummaryStatistics.RestrLogL | ISummaryStatistics.LRstatistic | ISummaryStatistics.LRprobability