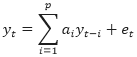
A unit root is a notion used in time series analysis that describes property of some non-stationary time series. The test name is explained by the fact that roots of the characteristic equation of time series autoregression model have the modulus equal to one.
Let there be an autoregressive model:
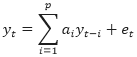
Using the lag operator L: Lxt=xt-1 this model can be written down as follows:
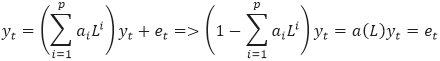
Characteristic polynomial of this model is a polynomial of the following type:
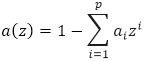
Roots of this polynomial (roots of characteristic equation a(z)=0) in a general case are complex values. If all roots of this polynomial lie outside a unit circle of a complex plane (that is, have a modulus strictly greater than one), the autoregressive process is stationary. If modulus of some roots equals to one (theoretically there can be roots less than one), the autoregressive process is non-stationary.
Consider a model of the process Ar(1):
![]()
where yt - the tested series, xt - exogenous regressor that can contain a constant, a trend, or a constant and trend, ρ and δ – estimated parameters, and ut - model residuals. There is a number of tests for unit roots:
Generalized Dickey-Fuller test.
Phillips-Perron test.
Kwiatkowski-Phillips-Schmidt-Shin test.
Elliott-Rothenberg-Stock test.
Ng-Perron test.
See also: