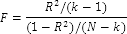
Fisher statistics is used to check the hypothesis of the correlation between an output variable and regressors. The null hypothesis of coefficients' equality to zero for all regressors is analyzed.
Formula for Fisher statistics calculation for a model with a constant:
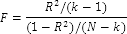
Formula for Fisher statistics calculation for a model without a constant:
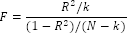
Where:
k. The number of factors included into the model (including a constant).
N. Number of observations.
For uncentered determination coefficient corresponding Fisher statistics can be calculated.
The Fisher statistics has the Fisher distribution:
For a model with a constant: F(k - 1, N - k).
For a model without a constant: F(k, N - k).
The null hypothesis on the coefficients equality to zero for all regressors is rejected if the probability is less than the significance level. One of standard significance levels (0.1, 0.05 or 0.01) is considered.
See also:
ISummaryStatistics.Fstat | ISummaryStatistics.Fstat_2 | ISummaryStatistics.ProbFstat | ISummaryStatistics.ProbFstat_2 | ISmARCHTest.FStatistic | ISmBreuschPaganGodfreyTest.FStatistic | Library of Methods and Models