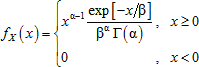
Gamma distribution that has parameters α, β > 0 is described with probability density function:
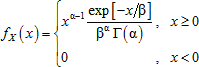
Where the function Г(α) looks as follows:
![]()
When modeling random values X ~ Г(α, β) scaling of gamma distribution by the parameter β is taken into account. First, the model X1 ~ Г(α, 1) is created for β = 1, to move to gamma value with other values of the β parameter, it is required to multiply X = β·X1.
To generate values from the distribution Г(α, 1), one can use three algorithms, each of which is valid at its range of α values:
0 < α < 1. The Ahrens and Dieter algorithm (1974) is applied and follows the next steps to generate each gamma value:
The value is generated from the standard equal distribution u1 ~ U(0, 1), and values of b = (exp + α) / exp are also calculated, as well as P = b·u1. If P > 1, go to the step 3. Otherwise, go to the step 2.
Assume that Y = P1/α, then generate the value u2 ~ U(0, 1). If u2 ≤ exp[Y], the value X = Y is returned. Otherwise, return to the step 1.
Assume that Y = –ln [(b – P)/α], then generate the value u2 ~ U(0, 1). If u2 ≤ Yα – 1, the value X = Y is returned. Otherwise, return to the step 1.
α = 1. Execute an algorithm based on the fact that the distribution Г(1, 1) is an exponential distribution with the mean equal to one. In this case the pseudo-random value X ~ Г(1, 1) is generated using the inverse transformation method, that is, the following sample is calculated based on the inverse function of exponential distribution: X = –ln U, where U ~ U(0, 1) – random value, uniformly distributed at the interval (0, 1).
α > 1. The Cheng's algorithm (1977) modified by Law and Kelton executes the following steps to generate each gamma value:
Calculate values of constants: ![]() , b = α – ln 4, q = α + 1/α, Q = 4.5 and d = 1 + ln Q.
, b = α – ln 4, q = α + 1/α, Q = 4.5 and d = 1 + ln Q.
Generate two independent values u1 and u2 from standard uniform distribution U(0, 1).
Assume that V = a ln [U1/(1 – U1)], Y = α exp[V], Z = U12 U2 и W = b + qV – Y.
If W + d – QZ ≥ 0, X = Y is returned. Otherwise, go to the step 5.
If W ≥ ln Z, the value X = Y is returned. Otherwise, go to the step 2.
See also: