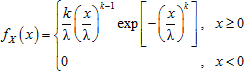
Двухпараметрическое распределение Вейбулла с параметрами формы k > 0 и масштаба λ > 0 характеризуется функцией плотности вероятности:
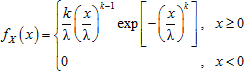
Для моделирования случайных величин использован метод обратного преобразования, позволяющий при наличии генератора выборки из стандартного непрерывного равномерного распределения получить выборку из распределения Вейбулла. Используется свойство, что если случайная величина U ~ U(0, 1) распределена равномерно на отрезке (0, 1), то случайная величина X = λ(ln(U))1/k имеет распределение Вейбулла W(k, λ) с параметрами k и λ. Генерирование выборки x1, …, xn производится путём выполнения следующих операций:
Генерирование выборки u1, …, un псевдослучайных чисел из стандартного непрерывного равномерного распределения на интервале (0, 1).
На основании обратной функции 
, а также
с учетом того факта, что величины U
и 1 – U имеют одно
и то же распределение U(0, 1),
вычисляется выборка из искомого распределения Вейбулла по формуле:
См. также:
IStatistics.Weibull | ISmWeibullDistribution | Библиотека методов и моделей