Метод Монте-Карло

Метод используется для расчёта модели VaR.

Для каждого финансового инструмента, участвующего в расчете, выбирается распределение:

• нормальное (гауссовское) распределение;

• распределение Стьюдента;

• распределение Хи-квадрат;

• двустороннее экспоненциальное распределение;

• распределение Вейбулла;

• гамма-распределение;

• равномерное распределение.

Финансовые инструменты могут иметь разные распределения.

В зависимости от распределения, генерируются коррелированные случайные величины по каждому финансовому инструменту. Матрица сгенерированных случайных величин:

R = ǁRk,jǁ

Где:

• k. Количество испытаний;

• j = 1, 2, … M. Количество финансовых инструментов, участвующих в расчете.

Формула расчета Rk,j зависит от вида распределения:

• нормальное (гауссовское) распределение

Rk,j - псевдослучайное число, распределенное по нормальному закону со средним bj и стандартным отклонением dj.

• распределение Стьюдента

Rk,j - t-значение распределения Стьюдента со случайной вероятностью (от 0 до 1) и степенью свободы равной 2.

• распределение Хи-квадрат

Rk,j - псевдослучайное число, распределенное по закону Хи-квадрат со степенью свободы 1.

• двустороннее экспоненциальное распределение

Для каждого финансового инструмента из матрицы доходности считаются:

1. • xj - количество элементов меньше нуля;

   • yj - количество элементов больше нуля;

   • zj - количество элементов равных нулю;

   • xj - среднее по отрицательным элементам;

   • yj - среднее по положительным элементам;

Если средние не учитываются, то zj всегда считается равным нулю.

Для генерации значений Rk,j считаются вспомогательные значения:

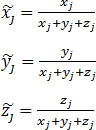
Для каждого k генерируется случайное число t от 0 до 1.

Если , то Rk,j - экспоненциальное распределение с интенсивностью .

Если , то Rk,j равняется нулю, иначе Rk,j экспоненциальное распределение с интенсивностью .

• распределение Вейбулла

Rk,j - псевдослучайное число, распределенное по закону Вейбулла с параметрами dj и bj, а именно, значение , где p - это псевдослучайное число, равномерно распределенное на промежутке от 0 до 1.

• гамма-распределение

Rk,j - обратное гамма распределение со случайной вероятностью p (от 0 до 1).

• равномерное распределение

Rk,j - случайное число, равномерно распределенное между началом промежутка dj (включая его) и концом промежутка dj (исключая его).

- средние значения финансовых инструментов.

- стандартные отклонения по выборке финансовых инструментов.

Если используется факторизация Холецкого, то из матрицы корреляций COR формируется матрица Холецкого - H. Каждая строка матрицы R умножается на матрицу Холецкого по правилам умножения вектора-строки на матрицу. Полученный вектор заменяет строку матрицы R.

Расчёт VaR производится историческим методом, но вместо матрицы доходности используется сгенерированная матрица R.

Выходным параметром является матрица VaR = ǁVaRlǁ, содержащая VaR портфеля каждой организации, участвующей в расчете.

См. также:

Value-At-Risk