Квантильная регрессия - процедура оценки параметров линейной зависимости между объясняющими переменными и заданным уровнем квантили объясняемой переменной. В отличие от обычного метода наименьших квадратов, квантильная регрессия является непараметрическим методом. Это позволяет получить больше информации: параметры регрессии для любых квантилей распределения зависимой переменной. Кроме того, такая модель значительно менее чувствительна к выбросам в данных и к нарушениям предположений о характере распределений.
Пусть Y - случайная переменная с функцией распределения вероятностей F(y) = Prob(Y ≤ y). Тогда квантилем уровня τ, где 0 < τ <1, будет являться наименьшая величина Y, удовлетворяющая условию F(y) > τ:
Q(τ) = inf{y:F(y) ≥ τ}
Учитывая набор n наблюдений по переменной Y, традиционная эмпирическая функция распределения определяется по формуле:
![]()
Где I(Yi < y) индикатор функции, который дает значение 1, если аргумент принимает значение ПРАВДА и 0, если ЛОЖЬ.
Соответствующий эмпирический квантиль определяется по следующей формуле:
Qn(τ) = inf{y:Fn(y) ≥ τ}
Эквивалентна запись в виде задачи оптимизации:
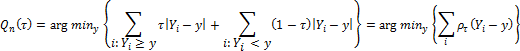
Где ρτ(u) = u(τ - I(u < 0)) - функция, по-разному взвешивающая положительные и отрицательные значения Yi - y.
Квантильная регрессия расширяет данную задачу, позволяя учитывать регрессоры.
Пусть условные квантили заданных значений переменной Y линейно зависят от вектора объясняющих переменных Х:
Q(τ|Xi,β(τ)) = X̕i,β(τ)
Где β(τ) - это вектор коэффициентов, соответствующих квантилю τ. Тогда задача безусловной минимизации выглядит следующим образом:
![]()
Данная задача решается с помощью модифицированного симплекс-метода.
Один из вариантов оценки разреженности наблюдений:
s(τ) = X*'(β(τ + h) - β(τ - h))/(2h), где:
τ. Квантиль;
X*. Вектор значений объясняющих переменных;
h. Окрестность, для которой рассчитывается разряженность наблюдений.
В простейшем случае: X* = X̅ - вектор средних значений объясняющих переменных.
h вычисляется по формуле:
 ,
,
где zα = Φ-1(1 - α/2), α – уровень значимости.
Для точного расчета матрицы необходимо значение разряженности наблюдений. При приближенной оценке оно не требуется.
Для расчёта обычной ковариации с помощью гипотезы НОРСВ (независимых одинаково распределённых случайных величин, англ. Ordinary(IID) covariance) используется формула:
cov(β) = s2(X'X)-1,
где s2 = τ(1 - τ)s(τ)2 - дисперсия ошибок.
Для вычисления необходимо рассчитать квантильную регрессию вида y = c, где c - константа. Минимальное значение целевой функции будет необходимым значением.
Для вычисления необходимо рассчитать квантильную регрессию, описанную выше.
Для вычисления необходимо рассчитать квантильную регрессию вида y = c, где c - константа. Оцененный коэффициент модели будет необходимым значением.
Рассчитывается по формуле:
Pseudo R2 = 1 - objective/restr.objective,
где:
objective. Значение целевой функции заданной модели;
restr.objective. Значение ограниченной целевой функции.
Рассчитывается по формуле:
![]() ,
,
где:
n. Количество наблюдений;
k. Количество коэффициентов модели, включая константу.
См. также: