 ,
,OddfPrice(Settlement: DateTime; Maturity: DateTime; Issue: DateTime; FirstCouponDate: DateTime; Rate: Double; YieldP: Double; Redemption: Double; Frequency; Integer; [Basis; Integer = 0]): Double;
OddfPrice(Settlement: System.DateTime; Maturity: System.DateTime; Issue: System.DateTime; FirstCouponDate: System.DateTime; Rate: double; YieldP: double; Redemption: double; Frequency; integer; Basis; integer): double;
Settlement. The payment day on securities. Must be greater than Issue.
Maturity. The security's maturity date. Must be greater than FirstCouponDate.
Issue. The security's issue date. Must be less than Settlement.
FirstCouponDate. Securities first coupon date. Must be greater than Settlement.
Rate. Annual interest rate for coupons on securities. Must be positive.
YieldP. The annual income on securities. Must be positive.
Redemption. The security's redemption price per $100 face value. Must be positive.
Frequency. The annual number of coupon payments. The parameter can take the following values:
1. Annual payments.
2. Semi-annual payments.
4. Quarterly payments.
Basis. The day calculation method used. Select a value from 0 to 4:
0. The day calculation method - American/360 days (NSAD method).
1. The day calculation method - Actual/actual.
2. The day calculation method - Actual/360 days.
3. The day calculation method - Actual/365 days.
4. The day calculation method - European 30/360 days.
The OddfPrice method returns price for 100 rubles of face value of the securities for an irregular - short or long - first period.
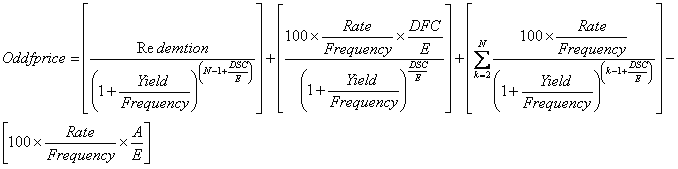
OddfPrice is calculated using the following formula.
Irregular short first coupon:
 ,
,
where:
A. The number of days from the beginning of the coupon period to the settlement date (accrued days).
DSC. The number of days from the settlement to the next coupon date.
DFC. The number of days from the beginning of the odd first coupon to the first coupon date.
E. The number of days in the coupon period.
N. The number of coupons payable between the settlement date and the redemption date. If this number contains a fraction, it is raised to the next whole number.
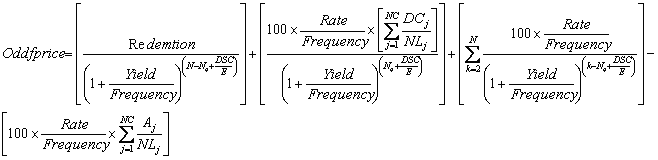
Irregular long first coupon:
 ,
,
where:
Aj. The number of days from the beginning of the j-th last quasi coupon period in the non-regular period.
DCj. The number of days from the specified date (or issue date) to the first quasi coupon (j = 1) or the number of days in the quasi coupon (j = 2,…, j = NC).
DSC. The number of days from the settlement to the next coupon date.
E. The number of days in the coupon period.
N. The number of paid coupons from the first actual coupon date to the maturity date. (If this number is fractional, it is rounded up to the next integer).
NC. The number of quasi coupon periods, which fits in an irregular period. If this number is fractional, it is rounded up to the next integer.
NLj. Normal length in days of the full j-th or last quasi coupon period in an irregular period.
Nq. The number of full quasi coupon periods from the settlement date to the first coupon.
Add a link to the MathFin system assembly.
Sub UserProc;
Var
r: Double;
Begin
r := Finance.OddfPrice(DateTime.ComposeDay(2008,11,11), DateTime.ComposeDay(2021,03,01),
DateTime.ComposeDay(2008,10,15), DateTime.ComposeDay(2009,03,01), 0.1275, 0.1025, 200, 4, 3);
Debug.WriteLine(r);
End Sub UserProc;
Imports Prognoz.Platform.Interop.MathFin;
…
Public Shared Sub Main(Params: StartParams);
Var
r: double;
Finance: FinanceClass = New FinanceClass();
DateTime1, DateTime2, DateTime3, DateTime4: System.DateTime;
Begin
DateTime1 := New DateTime(2008,11,11);
DateTime2 := New DateTime(2021,03,01);
DateTime3 := New DateTime(2008,10,15);
DateTime4 := New DateTime(2009,03,01);
r := Finance.OddfPrice(DateTime1, DateTime2, DateTime3, DateTime4, 0.1275, 0.1025, 200, 4, 3);
System.Diagnostics.Debug.WriteLine(r);
End Sub;
After executing the example the console window displays the price equal to 146.115.
See also: