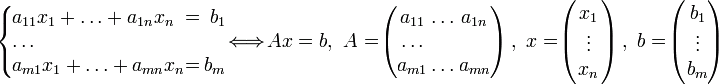 (1)
(1)Gauss method is a method for solving the system of linear algebraic equations (SLAE) that is gradual decrease of the system order and elimination of the unknown.
Solving the SLAE with the Gauss method consists of two steps:
During the first step (forward elimination): using elementary transformations on the rows, the system is reduced to echelon or triangular form, or it is established that the system is inconsistent. Select a non-zero element from the elements of matrix first column, move it to the top position using row permutation, and subtract the first row that is obtained after the permutation from other rows; first, the user needs to multiply this row by the value equal to the ratio of the first element of each row to the first element of the first row, thus, nulling the column under this element. Then the first row and column are mentally crossed out. Continue in this way until the null matrix is left. If a non-zero element is not found in the first column during one of the iterations, move to the next column and do the same.
The second step uses back-substitution. The point of this step is to express all the output basic variables through non-basic and construct a fundamental system of solutions. If all the variables are basic, it is necessary to express the only solution of the linear equation system in numerical form. This procedure starts with the last equation. This equation is used to express the only corresponding basic variable to be substituted in the previous equations. Continue in this way going up the "stairs". Only one basic variable corresponds to each row, so at every step except for the last one the situation is the same as in case of the last row.
Suppose, there is an original system that looks as follows:
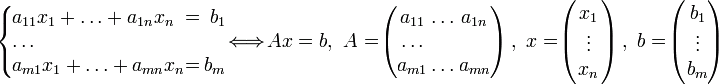 (1)
(1)
The A matrix is named the main matrix of the system, and the b matrix is named a column of free terms.
Using the property of elementary row operations, a basic matrix can be changed to an echelon matrix. The same operations should be applied to the column of free terms:
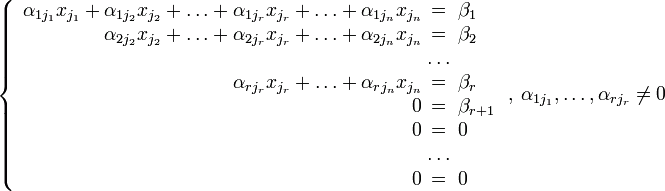
Suppose that the principal minor (non-zero minor of maximum order) of the main matrix is located in the upper left corner, that is, it contains only coefficients of the variables xj1, …, xjr. This position of the minor can be achieved using permutation of the main matrix columns and corresponding renumbering of variables.
Therefore, the variables xj1, …, xjr are named main variables. All other variables are named free variables.
If at least one number βi ≠ 0, where i > r, the considered system is incompatible.
Suppose that βi = 0 for any i > r.
Transfer free variables outside the equality signs and divide each of the system equations by its coefficient at the leftmost ![]() (αij, i = 1, …, r, where i is the row number):
(αij, i = 1, …, r, where i is the row number):
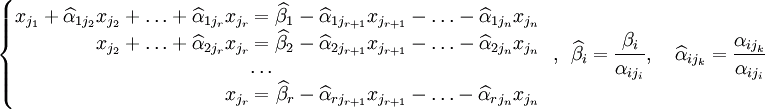 (2)
(2)
Where i = 1, …, r, k = i + 1, …, n.
If all possible values are assigned to free variables of the system (2) and the new system is solved in regard to principal unknown quantities bottom-up (that is, from lower equation to top one), as a result, all solutions of this SLAE are obtained. As this system has been obtained by executing the elementary transformations on the source system (1), then in accordance with the theorem of equivalency during elementary transformations, the systems (1) and (2) are equivalent, that is, the sets of their solution coincide.
Effects:
If all variables of a collocated system are the master variables, the system is a definite one.
If the system has more variables than equations, the system can be either indefinite or incompatible.
See also: