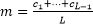Trend with Functional Dependency Estimation
Trend
A trend is a non-random slowly changing component of a time series, which is affected by random fluctuations or seasonal effects.
As a rule, to determine trends for short-time series, parametric methods are used. In this case a time series is presented as a sum of determinate time function F (t,a) (a - unknown parameter vector), that depends on a few unknown parameters, and the random component err(t). Thus, if the frequency of the studied process is the time series Y(t), where t = 1, …, N, the trend model looks as follows:
Y(t) = F(t, a) + err(t)
Where:
Types of Functional Dependencies
The vector of unknown parameters a is estimated using least-squares method. To apply this method, the function F (t, a) must be of linear type or should be able to linearize (cast to linear type).
Main types of dependencies:
Seasonality
Seasonality is a time series component that shows repeated economic processes during small time periods, usually it is the influence of external factors that affect the data cyclically with a predetermined frequency.
A time series and its fluctuations can be presented in various ways: with additive seasonality coefficient or multiplicative seasonality coefficient. Thus, the non-random series component is decomposed to two components:
Where:
P(t). Trend without seasonal factor belonging to the selected parametric family.
S(t). Seasonal component (seasonality coefficient) is assumed to be periodic with the integer seasonal period L, that is, S(t) = S(t + L).
Seasonality Calculation Methods
Additive seasonality is taken into account by means of the method of dummy variables. The method consists in adding of dummy variables into a model, each of the dummy variables indicates whether observation belongs to a certain season.
y = F(t, a) + c1s1 + c2s2 + … + cL-1sL-1
Where:
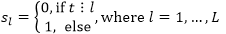
The number of dummy variables should be less by one than that of the season, because coefficient for the last season is precisely determined based on values of coefficients for other seasons.
After model coefficient estimates are obtained, it is required to convert calculation of seasonal components based on the condition:
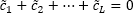
A total model of trend calculation with additive seasonality looks as follows:
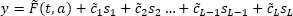
Where:
This method of seasonality estimation can be applied to linear models. If a source model requires linearization, this method is used to determine multiplicative seasonality.
To take multiplicative seasonality into account, the Census1 method is used in linear models. This method enables the user to exclude seasonality before estimating model trend coefficients. If a source model requires linearization, this method is used to determine additive seasonality.
See also:
Modeling Container: The Trend with Functional Dependency Estimation Model | Time Series Analysis: Trend | IModelling.Extrapolate | IEmCurveEstimationSettings | ISmCurveEstimation
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.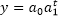 will be converted to linear function
will be converted to linear function 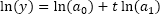 or
or 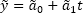 . OLS estimates are searched for parameters
. OLS estimates are searched for parameters 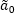 ,
, 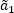 , and source parameters are obtained by means of inverse conversion:
, and source parameters are obtained by means of inverse conversion: 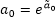 ,
, 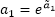 .
.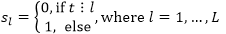
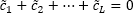
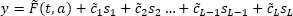
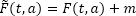
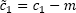
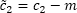
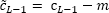
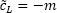 , where
, where