Missing Data Treatment

Missing data treatment fills in empty series values using various methods of missing data treatment.

Let we have M observations {x1, x2, …, xM} of the data series X. Some of the observations are missing, that is, corresponding Xi contain no data. Data may be missing in any position: at the beginning or end of the sample, there can be a single missing observation, or a continuous series of missing data.

Let us use the following symbols:

M. Total number of values in the sample.
i. The number of observation in the source sample, i = 1, …, M.
m. Number of non-empty values in the sample.
x. Minimum series value.
x̄. Maximum series value.
xi. The previous non-empty value nearest to the missing xi.
x̄i. The following non-empty value nearest to the missing xi.
ni. The number of missing data between xi and xi.
ZeroIfNoData(xi) = xi. If the observation xi contains some data.
ZeroIfNoData(xi) = 0. If the observation xi does not contain any data.
IsObserved(xi) = 1. If the observation xi contains some data.
IsObserved(xi) = 0. If the observation xi does not contain any data.

Available methods:

Average. Missing data is substituted with the arithmetic mean of the non-empty sample values:

N-Point Average. The missing data is substituted with arithmetic mean of N nearest non-empty values before and after the missing data:

If the calculating interval falls outside the array range, the average is calculated based on the available observations.

Previous Value. The missing data is substituted with the previous non-empty values:

Succeeding Value. The missing data is substituted with the next non-empty values:

Linear Interpolation. Missing data between neighboring non-empty values is substituted proportionally following the rule:

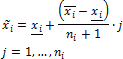
Linear Trend. Observations of the source series are assumed to be linearly dependent on their sequence number. Based on this assumption, a regression of the source series trend is formed by the available data. Then the missing data is substituted according to the estimated dependency:

where a0, a1 – estimated coefficients of the linear trend.

Random Value. Missing data is substituted with random values that belong to the range [x; x¯]:

where Randbetween is the function that generates random values that belong to the specified range.

Casewise. This method of missing data treatment uses for calculation only the observations of the source data array that contain no missing data.
Geometric Interpolation. The missing data is substituted by the following formula:

Value. The missing data is substituted with the specified value A.
Cubic Spline Interpolation. The missing data is substituted using cubic splines. Calculation of cubic splines is described in the Interpolation section.
Pattern. An auxiliary series without missing data is used as the pattern. The missing data in the source series is substituted proportionally to changes in the values of the pattern series (Pattern):

Overlay. An auxiliary series without missing data is used as the pattern. The missing data in the source series is substituted with the values of the pattern series:

Growth Rate to Specified Number of Succeeding Periods:
- One period: x(t) = x(t+1)/(1+pch(x(t+1))).
- Two periods: x(t) = x(t+1)/(1+average(pch(x(t+2)),pch(x(t+3)))).
- Three to n periods: x(t) = x(t+1)/(1+Average(pch(x(t+2)),pch(x(t+3)),pch( x(t+4)),…pch(x(t+n))).

Where: pch(x(t))=(x(t)/x(t-1)-1)*100.

Growth Rate to Specified Number of Previous Periods:
- One period: x(t) = x(t-1)/(1+pch(x(t-1))).
- Two periods: x(t) = x(t-1)/(1+average(pch(x(t-2)), pch(x(t-3)))).
- Three to n periods: x(t)=x(t-1)/(1+Average(pch(x(t-2)), pch(x(t-3)),pch( x(t-4)),…pch(x(t-n)))).

Where: pch(x(t))=(x(t)/x(t-1)-1)*100.

Missing Data Treatment Methods

The Geometric Interpolation method may leave treated missing data if the values of xi and x¯i have different sign, or at least one of these values is zero.

The methods Overlay and Pattern of missing data treatment may leave missing data if the specified series contains missing data or is empty.

The methods Growth Rate to Specified Number of Succeeding Periods and Growth Rate to Specified Number of Previous Periods may leave missing data if the specified range of previous or succeeding periods (based on which the growth rate is calculated) also has missing data.