Функция плотности многомерного нормального распределения для любого вектора x в d-мерном пространстве определяется как:
Где:
μ = (μ1, μ2, …, μd)T. Вектор средних значений;
Σ. Ковариационная матрица с (i, j)-м элементом Σij = Cov(Xi, Xj). Поэтому Σ является симметричной и положительно определенной;
|Σ|. Определитель матрицы Σ;
Σ-1. Матрица, обратная Σ.
Поскольку матрица Σ является симметричной и положительно определенной, то её можно разложить на множители Σ = CCT (так называемое разложение Холецкого), где матрица C с числом строк и столбцов d×d является нижним треугольником. Приняв обозначение, что cij является (i, j)-м элементом матрицы C, то алгоритм для генерирования искомого вектора X с нормальным многомерным распределением будет иметь следующий вид:
Выполнение разложения Холецкого матрицы Σ для нахождения такой матрицы C, которая удовлетворяет условию Σ = CCT, является нижней треугольной и содержит строго положительные элементы на диагонали:
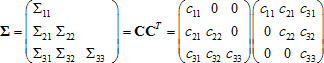
Элементы матрицы C вычисляются по следующим формулам:
при j < i:
Генерирование выборок Z1, Z2, …, Zd из независимых и одинаково распределенных величин с распределением N(0, 1), каждая выборка содержит по n элементов. При этом используется метод Бокса-Мюллера (см. описание нормального распределения).
Принять для i = 1, 2, …, d:
Возвращается значение X = (X1, X2, …, Xd)T. В матричной записи X = μ + CZ.
См. также:
ISmMultiNormalDistribution | Библиотека методов и моделей