Сингулярный спектральный анализ (англ. Singular spectrum analysis, SSA) относится к непараметрическим методам анализа временных рядов. Целью метода является разложение временного ряда на интерпретируемые аддитивные составляющие. Метод не требует стационарности ряда, знания модели тренда, а также сведений о наличии в ряде периодических составляющих. При таких слабых предположениях метод может решать различные задачи, например, выделение тренда, обнаружение периодичной составляющей, сглаживание ряда.
Из-за отсутствия модели отсутствует возможность проверить гипотезу о наличии в ряде той или иной составляющей, но на основе информации, получаемой с помощью анализа, можно построить параметрическую модель для проверки гипотез.
Базовый алгоритм метода состоит из двух дополняющих друг друга этапов: разложение и восстановление.
Пусть F = (f1, …, fn) - вещественный временной ряд длины N (N > 2 ). Ряд F - ненулевой, то есть существует хотя бы одно i такое, что fi ≠ 0.
Вложение
На этом шаге исходный временной ряд преобразуется в последовательность многомерных векторов.
Пусть L - длина таких векторов: целое число, определяемое пользователем (1 < L < N). Процедура вложения образует K = N - L + 1 векторов вложения
![]()
Таким образом, получаем L-траекторную матрицу ряда F: X = [X1; …; XK], которая состоит из векторов вложения в качестве столбцов.
Сингулярное разложение
Пусть S = (1/K)XXT. Пусть λ1; …; λL - собственные числа матрицы S, взятые в неубывающем порядке (λ1 ≥ … ≥ 0); U = [U1; …; UL] - ортогональная система собственных векторов матрицы S, соответствующих собственным числам.
Матрицу U можно рассматривать как матрицу перехода к главным компонентам XU = Y = (y1, …, yL).
Выделение главных компонент
В силу свойств матрицы U возможно представить матрицу ряда X как X = YU'. Таким образом, получаем разложение матрицы ряда по главным компонентам. Разложение можно получить, используя не все главные компоненты, а только те, которые несут большую часть информации о ряде. В этом случае столбцы матрицы Y, соответствующие незначимым компонентам, будут заполнены нулями.
Восстановление одномерного ряда
Восстановление производится путем процедуры диагонального усреднения.
Положим L* = min(L, K), K* = max(L, K), где L x K - размерность матрицы X. Тогда пусть x*ij = xij, если L < K, и x*ij = xji иначе. Процедура диагонального усреднения переводит матрицу X в результирующий ряд G = (g0, …, gN-1) по формулам:
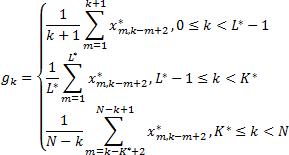
Таким образом, базовый алгоритм позволяет сгладить исходный ряд F, отбросив его случайную составляющую (шумы).
См. также: